Attenuation of scattering caused by thermal motion ↩

aliases: []
shorthands: {}
created: 2021-10-31 23:36:14
modified: 2022-01-10 04:13:04

Let's consider a crystal with finite temperature (for the sake of simplicity let it have only one atom in its unit cell). In this crystal, the position of atoms depends on time: . Let us assume that the components of the displacement vector are independent random variables with a normal distribution:

The temperature dependence is encoded in the standard deviation of the distribution. On higher temperatures, the deviation is larger, but we do not specify the exact temperature dependence here.

With these random displacements, the scattering amplitude and the intensity take these forms:

In order to determine the scattering pattern, we have to average out the randomness of the thermal motion:

Now we need to determine as a closed expression:

• If : due to the independence of the random variables
  Where the individual expected values are:

• If : then

These findings expressed using Kronecker deltas:

Then if we substitute this into the expression of the intensity, we get:

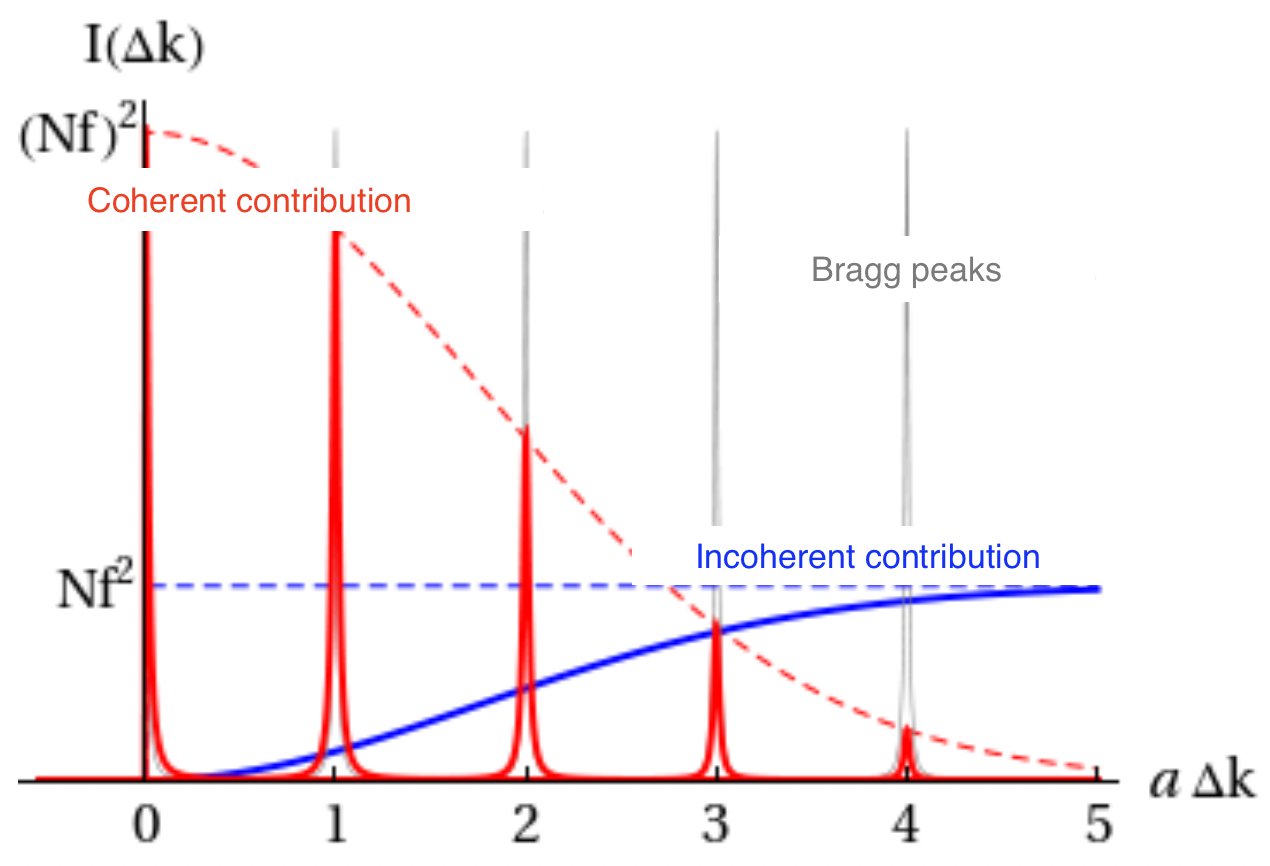
As we can see, the new intensity can be divided into two parts:

• The incoherent part that is nonzero at every wavenumber:

• The coherent part that is only nonzero at the reciprocal lattice vectors (pretty much modulates them):

We call the Debye-Waller factor.

How these contributions add up usually in the scattering pattern: